【図解】素数とDiffie-Hellman鍵交換法 ~わかりやすい計算例とシーケンス,RFCや種類,アルゴリズムについて~

Diffie-Hellman 鍵共有とは

IP ネットワーク通信において、暗号化による機密性と認証による通信相手の正当性を担保する技術として「IPsec」や「SSL/TLS」、「SSH」等があります。

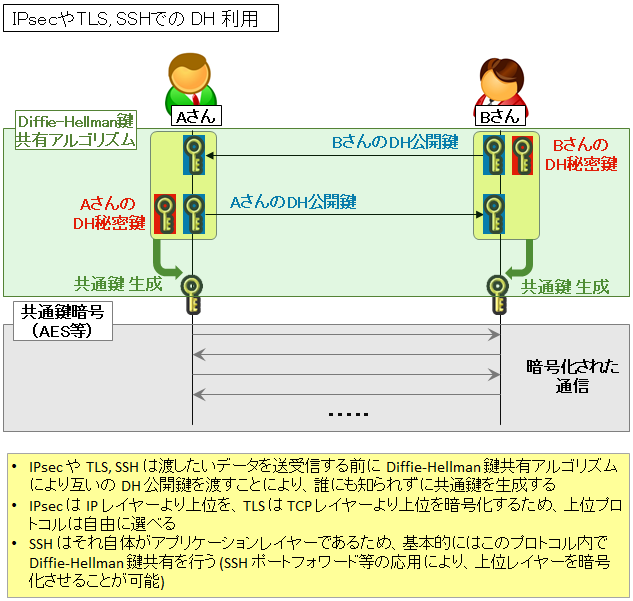
この 3 つのプロトコルは用途によって使い分けられますが、いずれも共通鍵暗号方式での通信暗号化のための「共通鍵の共有」を、【Diffie-Hellman 鍵共有 (DH 鍵共有)】というアルゴリズムによって実現します。

DH 鍵共有 (あるいは DH 鍵交換) とは、離散対数問題 (DLP : Discrete Logarithm Problem) という逆算の困難性を利用したアルゴリズムです。

DH 鍵共有の原理の理解に必要な基礎知識 : mod 演算 (剰余演算)

数学にはガウスが発明した mod 演算というものがあります。これはある数字で割り算したときの余り (剰余) に着目するものです。もともとは整数論として確立され、それが暗号理論に応用されています。

例えば 50 を 7 で割り算した時の余りは 1、324 を 7 で割り算した時の余りは 2 ですから

と表現します。この剰余演算は普通の計算と同じような、以下の性質があります。

• (a mod n) + (b mod n) = (a+b) mod n
• (a mod n) - (b mod n) = (a-b) mod n
• (a mod n) × (b mod n) = ab mod n
• (a mod n)^b mod n = a^b mod n

割り算も条件付きで定義可能ですが、ここでは省略します。

• (50 mod 7) + (324 mod 7) = 374 mod 7 = 3
• (50 mod 7) - (324 mod 7) = -274 mod 7 = 6
• (50 mod 7) × (324 mod 7) = 16200 mod 7 = 2

素数と離散対数問題 (Discrete Logarithm Problem)

n を「法」と呼びますが、n が素数のとき、ある整数のべき乗の剰余演算に面白い法則があります。

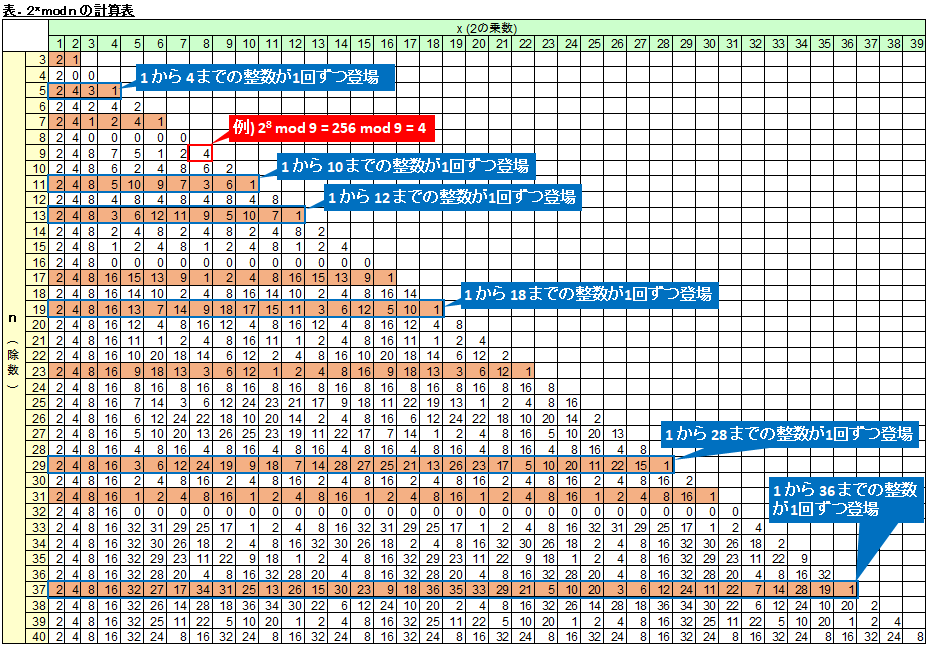
以下の表 (2^x mod n, 1 ≦ x ≦39, 3 ≦ n ≦ 40) をご覧ください。(Excel の関数 =MOD(2^C$2,$B3) で作成)

n が素数のとき (7, 17, 23, 31 を除いて)、計算結果に 1 から n-1 までの全ての整数が登場します。

例えば n=37 のとき、1 から 36 が 1 回ずつ登場します。

また、そのようにならなかった n=7, 17, 31 についても、3^x mod n を計算すると同様に 1 から n-1 までの全ての整数が登場します。

このように、n が素数で、基数 g (前述の 2 とか 3 の部分) を適切な値に選ぶと、g^x mod n (1 ≦ x ≦ n-1) は 1 から n-1 までの整数が 1 回ずつ登場します。

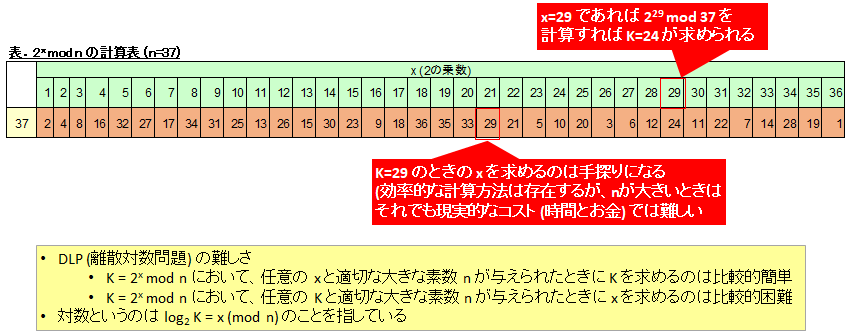
このようなとき、g^x mod n = K の計算で、K 以外の 3 つのパラメータが与えられていて K を計算するのは比較的簡単であるのに対し、x 以外の 3 つのパラメータが与えられて x を計算するのは難しい、という性質があります。

この x を求める難しい問題のことをDiscrete Logarithm Problem (DLP: 離散対数問題) と呼びます。

以降、mod n の n (法の n) が素数のとき、mod p と記述します。素数を英語で prime と呼ぶからです。

DH 鍵共有アルゴリズムでは、g (基数) と n 改め p (適切な大きな素数) を公開パラメータ、x (1 ≦ x ≦ p-1) を各個人の秘密鍵、K (g^x mod p) を各個人の公開鍵として使います。

g は小さくて構いませんが、p は大きい必要があります。繰り返しますが、g と p は公開パラメータなので周囲に既知で構いません。

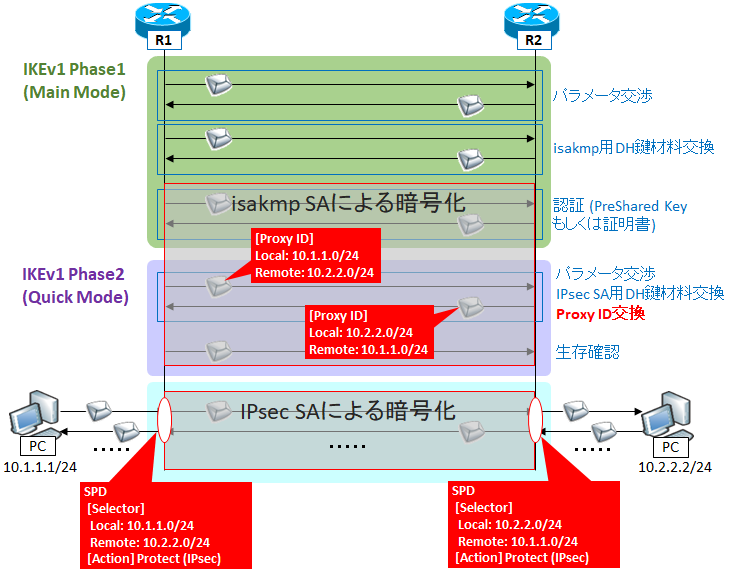
RFC2631 Section 2.2.1.2 では適切な g の選び方を紹介していますが、実装としては IPsec の DH-Group、SSL/TLS の supported-Groups などにおいて、g を 2 で固定し、素数 p を適切に選んで DH グループを定義しています。

なので簡単のため、以降は g = 2 で説明します。また、前述の通り p は十分大きい必要がありますが、こちらも簡単のため、小さい値で説明します。

DH 離散対数問題の計算例とシーケンス

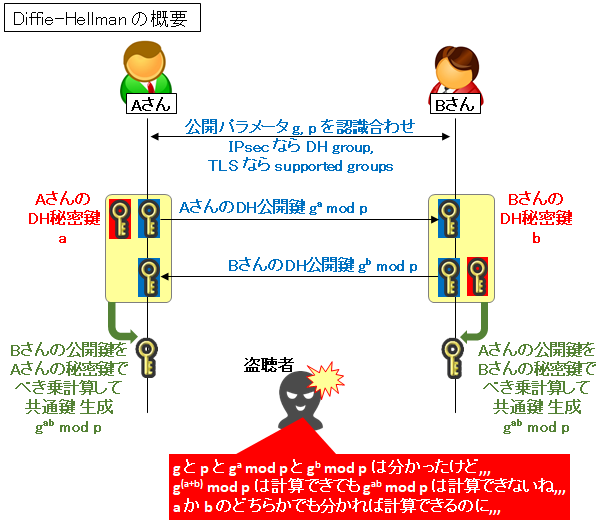
図で説明すると以下の通りになります。

例えば g=2, p=37, A の秘密鍵 a=23, B の秘密鍵 b=32 とします。

Diffie-Hellman の中間者攻撃とその対策

先程の例で、盗聴者への耐性を説明しましたが、Diffie-Hellman は「中間者攻撃 (MitM: Man in the Middle)」に弱いことが知られています。具体的な攻撃例は以下の通りです。

ただ、この対策として、たいていのプロトコル (IPsec, TLS, SSH 含む) ではデジタル署名により相手を認証することになっています。

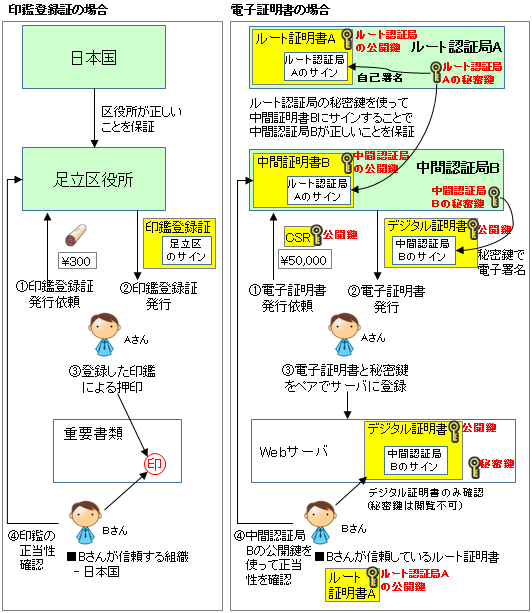
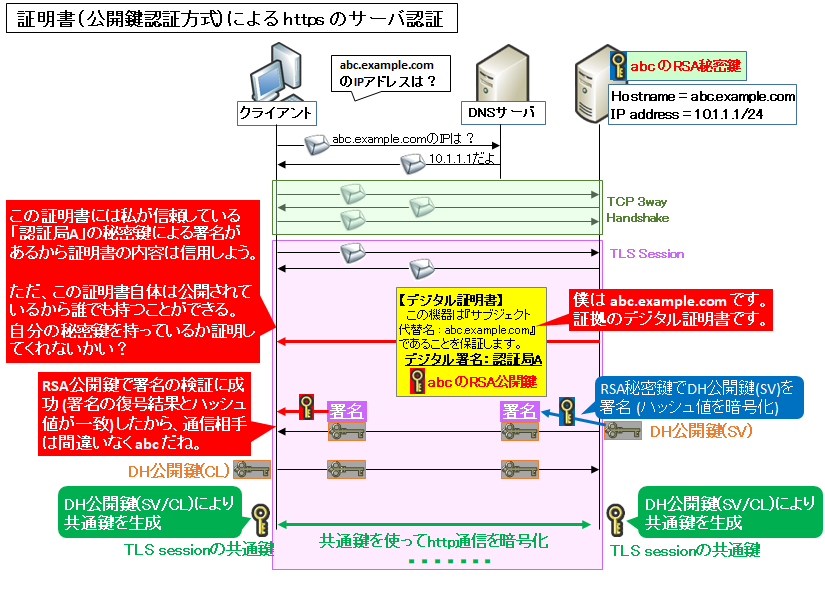
例えば TLS (https) においては、DH の公開鍵に対して、RSA 等の署名アルゴリズムを使ってデジタル署名を付加しています。この署名は相手が公開している公開鍵で検証できますが、その公開鍵が信頼できるかどうかについては、「デジタル証明書」のルート証明書が信頼されているかどうかを確認することによって検証します。

デジタル証明書や https の仕組みについては以下も併せてご参照下さい。

【図解】よく分かるデジタル証明書(SSL証明書)の仕組み 〜https通信フロー,発行手順,CSR,自己署名(オレオレ)証明書,ルート証明書,中間証明書の必要性や扱いについて〜

前提知識 デジタル証明書 (電子証明書) の理解のためにはまず RSA 公開鍵・...

milestone-of-se.nesuke.com

2020.10.30

Diffie-Hellman Group の RFC と IANA のページ

Diffie-Hellman の RFC には例えば以下があります。

• RFC2631 (基礎)
• RFC3526 (IPsec IKE DH group 関連)
• RFC7919 (TLS supported_groups 関連
• RFC8268 (SSH 関連)

こと、DH グループパラメータ (g,p) やその他パラメータに関する情報は IANA にまとまっています。

• IPsec (IKE) の DH group
• TLS の supported_groups
• SSH の KeyExchangeMethod

このページから RFC を辿ったほうが効率的でしょう。

Diffie-Hellman の種類, 用語関連

また、DH 用語についてもまとめておきます。

modp

MODular exponential with Prime の略で、一般的な Diffie-Hellman アルゴリズムを指します。楕円曲線暗号方式と区別するために、一般的な DH を modp と表現します。

FFDH (Finite Field Diffie-Hellman)

Finite Field (有限体) Diffie-Hellman の略で、こちらも modp と同じで、一般的な Diffie-Hellman アルゴリズムを指します。呼び方が異なるだけで、同じことを言っています。

ECDH (Elliptic Curve Diffie-Hellman)

Elliptic Curve Diffie-Hellman のこと。Elliptic Curve とは「楕円曲線」という意味です。modp (FFDH) と比べて短いビット数でも強固なセキュリティを実現する (逆算によりコストが掛かる) 方式です。

DHE, もしくは EDH

Ephemeral Diffie-Hellman のこと。Ephemeral とは「一時的」という意味です。

公開鍵をセッション毎に異なる値を使い、前方秘匿性を確保する方式です。

公開鍵を固定する方式「Static Diffie-Hellman」や「Ephemeral-Static Diffie-Hellman」と区別するときにこのように表現します。

SSL/TLS の Cipher-Suite の区別では DHE と後ろに E を付ける形で表記します。

FFDHE と記載されていたら Finite Field DH において Ephemeral な公開鍵を使う方式を指しますし、ECDHE と記載されていたら Elliptic Curve Diffie-Hellman において Ephemeral な公開鍵を使う方式を指します。

Static DH, もしくは Ephemeral-Static DH, もしくは Fixed DH

Static というのは「固定」という意味です。Ephemeral (一時的) の対となる言葉です。

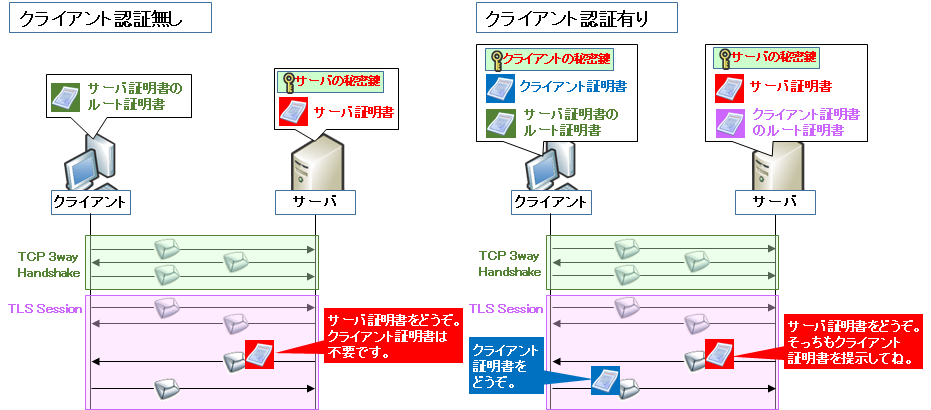
通信の片方 (主にサーバ側) の公開鍵について、常に同じものを使う方式です。サーバの証明書の中に固定の公開鍵を設定するのが一般的です。(TLS 1.3 以降では Static DH は廃止されていますが、S/MIME や OpenPGP で使われるケースがあります。)

片方が固定化される時点で、前方秘匿性は無くなります。(固定化された側の秘密鍵が漏洩した場合、過去に遡って共通鍵が明らかになる。)

SSL/TLS の暗号スイート (Cipher-Suite) の区別では DH とだけ記載されている場合は Static を指します。

DH と記載されていたら FFDH において Static な DH 公開鍵を使う方式を指しますし、ECDH と記載されていたら ECDH において Static な DH 公開鍵を使う方式を指します。

ただし、暗号スイート上の表現に関してはそうですが、それ以外のときに DH と出てきても、Ephemeral な DHE を指していたりするので、そのあたりは文脈から注意する必要があります。

IT/インフラエンジニアの地位とスキル向上のために

【年収UPの体験談】あなたの IT/インフラエンジニアとしての価値

IT 技術の進化はとどまることを知りません。矢継ぎ早に新たな技術が出てきたり、数...

milestone-of-se.nesuke.com

【パケットキャプチャ】はNWエンジニアの価値を大きく高める

nesuke の考える NW エンジニアの2つの道 ネットワークエンジニアには ...

milestone-of-se.nesuke.com