【図解】素数とRSA暗号/署名の仕組み ~わかりやすい計算例とシーケンス,アルゴリズム~

RSA とは
RSA の原理の理解に必要な基礎知識 : mod 演算 (剰余演算)
素数とカーマイケルの定理
RSA の計算例とシーケンス
おまけ『デジタル署名=秘密鍵で暗号化』というのは間違いなのか？
IT/インフラエンジニアの地位とスキル向上のために

RSA とは

IP ネットワーク通信において、暗号化による機密性と認証による通信相手の正当性を担保する技術として「IPsec」や「SSL/TLS」、「SSH」等があります。

この 3 つのプロトコルは用途によって使い分けられますが、いずれも通信相手の正当性を担保するための認証として「デジタル署名」を使います。

RSA はこのデジタル署名を実現する手段の 1 つです。RSA という名前は発明者の Rivest, Shamir, Adleman の頭文字に由来します。

昔は「共通鍵の交換」の仕組みとしても使われていましたが、「前方秘匿性が無い、つまり一度秘密鍵が漏洩したら過去の通信全てが解読されてしまう」方式であることから、最近では RSA を鍵交換用途では使われません。代わりに Diffie-Hellman 鍵交換が使われています。

RSA の公開鍵/秘密鍵がどのように使われるか、については以下の記事を参照下さい。

【図解】公開鍵・秘密鍵の仕組みを分かりやすく～公開鍵暗号方式の身近で具体的な利用例やメリット～

公開鍵暗号方式の種類と概要公開鍵暗号方式にはいくつか種類がありますが、この記事...

本記事では RSA の公開鍵/秘密鍵が数的にどのような仕組みになっているかを解説します。

RSA の原理の理解に必要な基礎知識 : mod 演算 (剰余演算)

数学にはガウスが発明した mod 演算というものがあります。これはある数字で割り算したときの余り (剰余) に着目するものです。もともとは整数論として確立され、それが暗号理論に応用されています。

例えば 50 を 7 で割り算した時の余りは 1、324 を 7 で割り算した時の余りは 2 ですから

50 mod 7 = 1
324 mod 7 = 2

と表現します。この剰余演算は普通の計算と同じような、以下の性質があります。

(a mod n) + (b mod n) = (a+b) mod n
(a mod n) - (b mod n) = (a-b) mod n
(a mod n) × (b mod n) = ab mod n
(a mod n)^b = a^b mod n

割り算も条件付きで定義可能ですが、ここでは省略します。

(50 mod 7) + (324 mod 7) = 374 mod 7 = 3
(50 mod 7) - (324 mod 7) = -274 mod 7 = 6
(50 mod 7) × (324 mod 7) = 16200 mod 7 = 2

素数とカーマイケルの定理

n を自然数 (正の整数) とし、m を n と互いに素の自然数とするとき、以下の式が成立します。

m^λ(n) mod n = 1 mod n

ただし、λ(n) は n を素因数分解したときの複数の素数から 1 減算したものに対する最小公倍数

これをカーマイケル (Carmichael) の定理と呼びます。また、λ (ラムダ) をカーマイケルのラムダ関数と呼びます。

例えば n= 35 としたとき、素因数分解すると 5*7 となるので、5-1=4 と 7-1=6 の最小公倍数は 12 なので

λ(35) = 12

となります。

m = 2 とした場合、n は奇数であれば m と n が互いに素となるので、 n を 3 ~39 の奇数とし、2^x mod n の計算をしてみましょう。(x は 1 ~ 39 の整数)

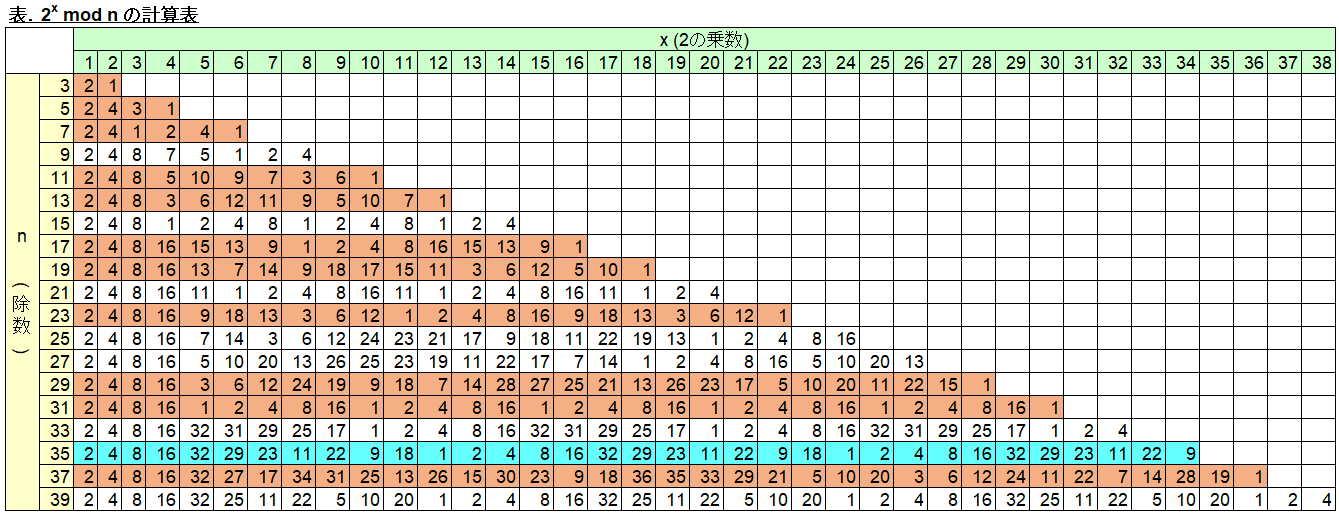
計算表の結果を以下に示します。(Excel の関数 =MOD(2^C$2,$B3) で作成)

n が素数の場合 (オレンジ網掛け) は 1 から n-1 まで全て互いに素となるので x = n-1 のときに 2^x-1 = 1 mod n となっていることが分かります。これはフェルマーの小定理と呼ばれているものです。

ですが、RSA に関してはここには着目せず、n が素数の掛け算の場合に着目します。例えば水色網掛けの n = 35 は、先ほど計算したとおり、2¹² mod 35 = 1 となっています。

m¹² = 1 になる、ということは、m¹³ = m になる、ということです。

つまり、元の数 m を mod n の下で累乗する場合、乗数には周期性があり (n=35 の場合は周期は 12)、例えば m を 31 乗して c になったとき、c を適切な乗数 a で累乗すれば m に戻る、ということです。(31a = 12b + 1 を満たす a を探す、ただし a, b は自然数)

この適切な乗数 a は「ユークリッドの互除法」を使えば探すことができます。計算方法はここでは割愛しますが、結果、a=7, b=18 となります。

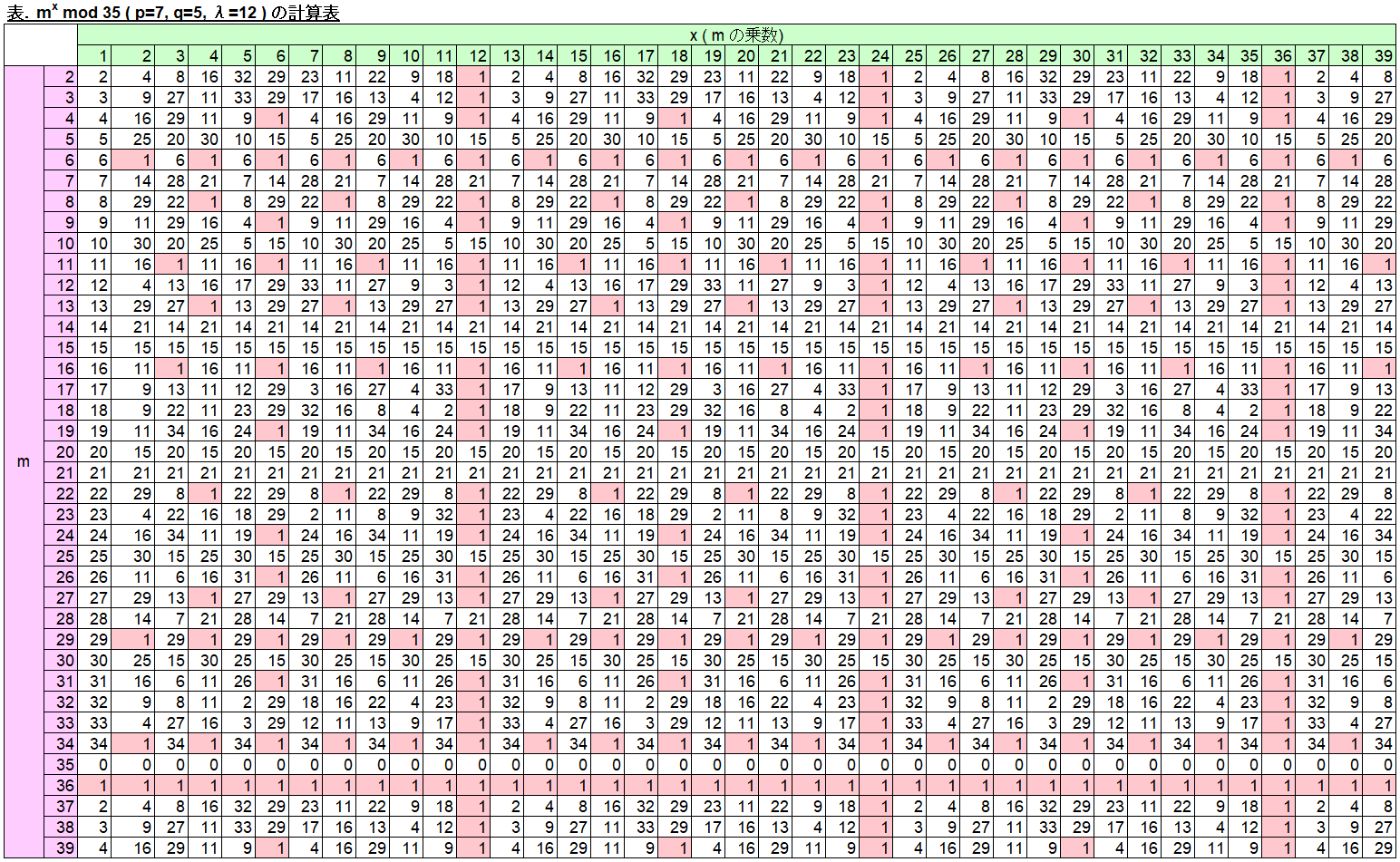
以下に n = 35 とした場合の、m が 2 ~ 39 のときの m^x mod 35 の計算表を示します。x = 12b + 1 のときに m に戻っていることが分かります。

これだとなんとなく簡単そうですね。では、n = 1357 とした場合はどうでしょう。

https://milestone-of-se.nesuke.com/static/rsa/RSA-n1357.html

どうでしょうか。4 桁になると直感的に難しさを感じたでしょうか。

1357 を素因数分解すると、23 * 59 となります。

λ(1357) = (23-1 = 22 と 59-1 = 58 の最大公倍数) = 2*11*29 = 638

となるので周期は 638 です。

ここで何となく勘付くかもしれませんが、RSA の仕組みの本質は『周期が分かる場合、つまり素因数分解ができる場合は、元に戻す乗数を算出できるが、周期が分からない場合、元の値に戻す乗数の算出が困難である』ことです。

RSA の計算例とシーケンス

A さんから B さんにメッセージ m = 508 を誰にも知られずに送ることを考えます。n = 1357 とします。

B さんは公開鍵 e と秘密鍵 d を、e*d mod 638 = 1 となるよう生成します。公開鍵 e は素数がよく使われます。例えばここでは e = 223、d = 103 とします。(223*103 = 638*36 + 1 = 22969)
公開鍵 e = 223 と n = 1357 を A さんに送ります。d は秘密にします。
A さんは送りたいメッセージ 508 を 223 乗して暗号化します。つまり、c = 508²²³ mod 1357 を計算し、B さんに送ります。
B さんは秘密鍵 d = 103 を使って c を 103 乗します。c^d = 508^223*103 mod 1357 = 508^638*36+1 mod 1357 となるため、(周期は 638 のため、) 元のメッセージ m = 508 に戻ります。

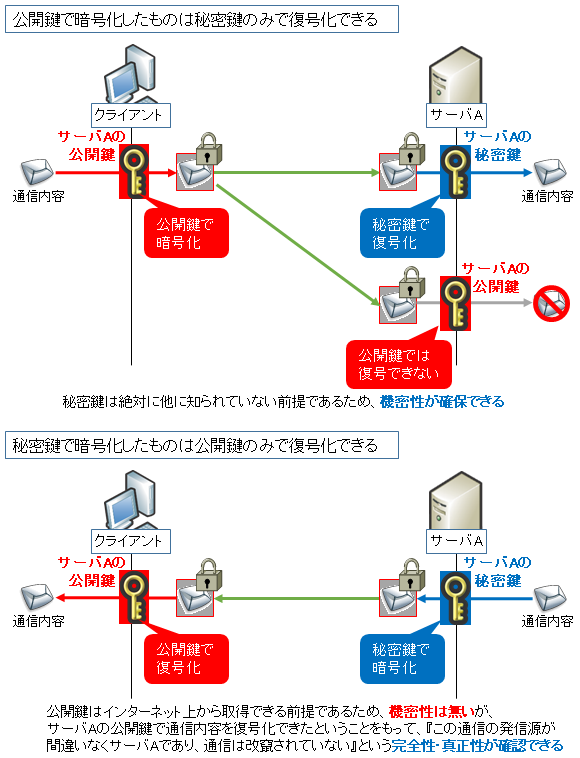
この構造が分かれば理解できると思いますが、メッセージ m を e 乗 (公開鍵で暗号化) したものに対しては d 乗 (秘密鍵で復号) することで元の m に戻りますし、メッセージ m を d 乗 (秘密鍵で暗号化) したものに対しては e 乗 (公開鍵で復号) することで元の m に戻るのです。

前者はメッセージの機密性を実現するための『RSA 暗号』、後者はメッセージの真正性 (デジタル署名) を実現するための『RSA 署名』となります。

これが RSA の大きな特徴です。

おまけ『デジタル署名=秘密鍵で暗号化』というのは間違いなのか？

デジタル署名を行うとき、メッセージを秘密鍵によって累乗するわけですが、このオペレーションをここでは暗号化と呼んでいます。

ところが、色々と調べものをしていた中で、『秘密鍵で暗号化というのは誤解であり、正しくは秘密鍵で復号である』との主張がありました。

あまり本質的な話では無さそうだなと思いつつ、色々と調べてみた結果、やはり本質的では無かったのですが、せっかく調べたのでおまけとして載せておきます。

結論としては、「どちらも間違いではない」です。

まず、その主張としては「RSA の論文として初期のアイディアとして『秘密鍵で復号して署名を行い、公開鍵で暗号化して検証する』となっていたので、それが正しい」とのことでした。

確かに RSA の論文 (1978年) には以下の文面がありました。

https://people.csail.mit.edu/rivest/Rsapaper.pdf

A message can be “signed” using a privately held decryption key.

ですが RFC2313 (1998年) を見てみると、10.1 Signature process のセクションで RSA encryption と記載されています。

10.1 Signature process
The signature process consists of four steps: message digesting, data encoding, RSA encryption, and octet-string-to-bit-string conversion.

ちなみに RFC2313 の著者は本家 RSA 所属の人です。

Burt Kaliski
RSA Laboratories East

ですが不思議なことに、以降の RFC2437 から RFC8017 まで、(こちらも著者は本家 RSA 所属の人が絡んでいるのですが、) Section 8 と 9 の Signature 関連のセクションに関して「Encryption」も「Decryption」も言葉自体が使われなくなりました。(encry や decry で検索しても Section 8 9 だけ見事に引っ掛かりません)

たぶん、どっちでも良かったんだと思います。本質はそこではないので。

また、この主張に対する反論として、上記 RFC の話もありましたが、その他にも「署名アルゴリズムとして md5WithRSAEncryption や sha1WithRSAEncryption というものが定義されている。(和訳するとそれぞれ md5 を RSA で暗号化、sha1 ハッシュを RSA で暗号化という意味)」「暗号化するときはパディングによる前処理を行う。それは署名時の秘密鍵のオペレーションでも行う」といった客観的な反論がいくつか見られました。

一方、別の主張として「この誤解が目に見えない足かせになる」というものもありましたが、事例や論拠に乏しくあまり客観的な主張では無いですし、そもそも誤解とも言い切れないのであまり取り立てて論争を起こすほうが逆に入門者は惑わされ足かせになるのではないでしょうか。

私にとってはこの話はカトリックとプロテスタント。ただ、私はプロテスタントを信仰しているだけ。どちらも間違いではないのです。