TCP segment format

The communication data unit of TCP is often referred to as "segment", we will call so here.

It shows the format of the TCP segment below.If TCP is used as IPv4 upper layer of, Ox06 (in decimal also 6) to the IPv4 protocol field specifies the.

For each Field
IT/インフラエンジニアの地位とスキル向上のために

For each Field

Source port

16bit. It is the port number to be used at the sender. If the sender is the client, more than 1024 called "Higher Port" in many scene will be used.

Destination port

16bit. It is the port number to be used at the receiver. If the destination is a server, it will be the port number in accordance with the service. For example, it is 80 if a http connection to the Web server, and it is 23 if a telnet connection to the telnet server.

The sequence number / acknowledgment number

Both 32bit. Whether it has received any data tells each other opponent. Retransmitting when detecting the received data not, such as helping to provide high reliability. In addition, even if has changed the arrival order of the TCP data, it is also assembled the data in the order.

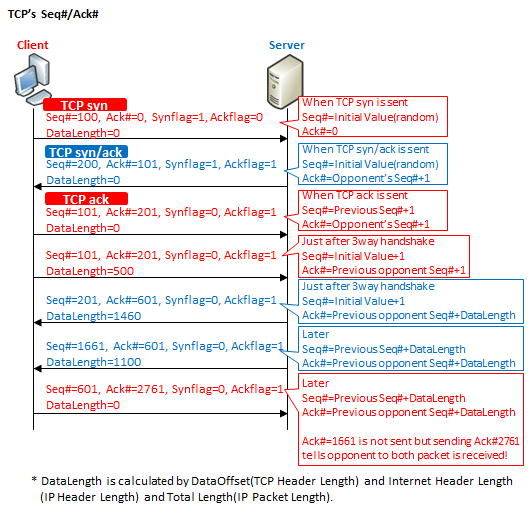
The following is an example of a change in the number of Seq#/Ack#.

The sequence number (Seq#), at the time of the TCP 3way handshake of TCP syn and TCP syn/ack transmission when put a TCP connection, terminal each, determines the initial value to the random.

Later it will be "Seq# = previous Seq# + the number of bytes of TCP data sent to the opponent (DataLength)". In exceptional cases, a packet of 3way handshake is DataLength = 0 actually, but calculated in DataLength = 1. It means "Seq# = previous Seq# + 1" while 3way handshake being done.

For example, in the Seq# = 101, when it sent the data of 500byte to the opponent, the next Seq# of the TCP segment to send will be 601.(TCP number of bytes of data is calculated DataOffset (TCP header length) and IP header length and the IP packet length)

It should be noted, Seq# will need to be independent in both directions. In other words, the Seq# in the direction of the client ⇒ server, Seq# in the direction of the server ⇒ client is different.

Acknowledgment number (Ack#) is, TCP syn will always be 0. Later it will be "Ack# = the last Seq# of opponent + received DataLength" but, in still exceptional, packet of 3way handshake is calculated in received DataLength = 1.

Since it is not efficient if acknowledgment is done for each segment, the receiver acknowledge some segments received at once when receive the segment certain number, by returning only Ack# for the last received segment. If there is a middle-deficient, divided into the following two patterns.

If you are in correspondence with the TCP option of SACK (Selective ACK), returns Ack# for the last received segment with "not-received Seq#" in the SACK field, will prompt a retransmission of the data of the missing Seq#.
If the SACK in does not support returns the Ack# of up to just before the loss, have them resend all the subsequent Seq# of data.

It should be noted that, whether or not correspond to the SACK is mutually notified by option at the time of the first TCP 3way handshake by "SACK permitted" option.

Data offset

4bit. The length of the TCP header (4Byte units) will enter.

CWR bit, ECE bit

Defined in RFC3268, is a bit for congestion control.

URG bit

In the case of 1, it indicates that it is an emergency communication.As is used the way, in the communication, which is defined as a "urgently" on the application side, set up the URG bit by using the socket API, you decide counterpart application is received it how to handle. It does not particularly do anything as TCP.

It seems little to use this bit and execute a special processing on the application side. And it seems no problem without too much consciousness. But if a case such as this bit is out in large quantities by running the packet capture, it is a good idea to inquire to the application vendor that made the communication.

ACK bit

In the case of 1, it indicates that the Ack# field is valid.

PSH bit

In the case of 1, the data receiving side will prompt immediately deliver the data to the application. This is also the same as the URG bit, make a bit by using a socket API on the application side, determines the processing in the counter application. It does not particularly do anything as TCP. You may feel that is often used than URG bit.

RST bit

If a host receives a TCP with this bit set to 1, the host must disconnects the TCP connection immediately.

This bit is set to 1 for return, for example, when the port of received TCP with syn is not open, or, when it receives the data which seems to be incorrect for the application.

SYN bit

This will be used for TCP 3way handshake in the first round trip. Not used in the other.

FIN bit

When there is no data to be sent to the sender, sent to the receiving side sets this bit to notify to close the connection. However, because the connection is the two directions, connection to each other sends the FIN bit from both basically will be completely finished.

Window

16bit. This Field as a way to indicate the number of bytes on the receiving side data acceptable to the sender.This Window Field when sending a segment that the receiving side has set the ACK bit to the transmitting side is also set.

It should be noted that this window Field, from the point of view of efficiency, an integer multiple of the MSS value has been good. In one sample, to the MSS of 1430Byte, 46 times the 65780Byte (= about 64KByte) it has been set (environment OS: Windows7, browser: IE9).

Checksum

16bit. The field in TCP header, not only TCP data, source IP address, destination IP address, protocol number (Ox06), are also checked TCP segment length.For more information, reliability of the checksum of TCP see the items.

Urgent Pointer

16bit. This field is valid only when the URG bit is set, it indicates whether there are things that need to be where the emergency processing in the TCP data.The value to be set in the Field is the location of the data required for the sequence number emergency treatment (in the sequence number is 110, if the data that requires emergency treatment was 440Byte from the beginning of the TCP data, enter 550).

As described above, the Field is how to take advantage of is up to the application, it does not particularly do anything as TCP.

The options are described in the next chapter.